Superelevation Trainz22
From TrainzOnline
(Difference between revisions)
(→Superelevation: how do you go about it?) |
(→For those who are curious...) |
||
| (90 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | The "superelevation" or the slope of rails in curves is proposed since T:ANE. '''This page updates the instructions for Trainz 22''' | + | == '''What is superelevation in Trainz 22?''' == |
| + | |||
| + | |||
| + | The "superelevation" or the slope of rails in curves is proposed since T:ANE. '''This page updates the instructions for Trainz 22'''<br> | ||
| + | '''Important to note : ''' The ‘Superelevation’ function worked very well with T:ANE and Trainz 2019. As of today (2024 october the 9th), it does not work with Trainz 22 and Trainz PE. | ||
| + | This error has recently been rectified and Superelevation is now available again, but for Trainz 22+ owners only. | ||
| − | |||
To resist centrifugal force and and not to wear out prematurely the outer rail, the track must be tilted on bends.<br> | To resist centrifugal force and and not to wear out prematurely the outer rail, the track must be tilted on bends.<br> | ||
| Line 32: | Line 35: | ||
<br><br> | <br><br> | ||
| − | = Surperelevation : theoritical base = | + | == '''Surperelevation : theoritical base''' == |
Everything that follows in this section is designed to give you the theoretical basis for calculating a superelevation. | Everything that follows in this section is designed to give you the theoretical basis for calculating a superelevation. | ||
In the next section, a spreadsheet will be provided to do all the calculations for you.<br><br> | In the next section, a spreadsheet will be provided to do all the calculations for you.<br><br> | ||
| − | * The <B>Superelevation</B> is the height that the outside rail takes compared with the internal rail in a curve. | + | * The <B>Superelevation</B> (SE) is the height that the outside rail takes compared with the internal rail in a curve. |
| − | It is calculated as the | + | It is calculated as the diagram below shows it:<br> |
| − | + | <table> | |
| − | + | <tr> | |
| − | * Of the four variables above (G, V, R,g), one is unknown at | + | <td>[[File:img396bis.jpg]]<td> |
| + | <span style="line-height:25pt;"> | ||
| + | 1 - <span style = "color:red;">Maximum value of SE</span> is limited to 16 cm (6.3 inches) for standard gauge tracks and 10 cm (3.14 inches) for metric tracks.<br> | ||
| + | 2 - <span style = "color:red;">Superelevation Limit</span> (or degree of slope <b><span style = "color blue";>A</span><span style = "font-size: 8pt;color:blue"> deg</span></b>) is limited to 6.4° for standard gauges and 5.8° for metric gauges.<br> | ||
| + | 3 - There is no superelevation for speeds lower than 25 kmh (15.5 mph) in standard gauge and 30 kmh (18.5 mph) in metrics.<br> | ||
| + | 4 - On networks with gauge of 60 cm (2 ft) or less, the speed is limited to 25 kmh (15.5 mph) : there is thus no superelevation either. | ||
| + | </span> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br><br><br> | ||
| + | * Of the four variables above (G, V, R,g), one is unknown at start: the <B>radius of the curve</B>. | ||
The diagram below shows how to determine it :<br> | The diagram below shows how to determine it :<br> | ||
[[File:img397bis.jpg]]<br><br> | [[File:img397bis.jpg]]<br><br> | ||
| + | |||
* Trainz 22 introduces an aditionnal concept for determining the superelevation of a curve: the <B>degree of curvature</B>.<br> | * Trainz 22 introduces an aditionnal concept for determining the superelevation of a curve: the <B>degree of curvature</B>.<br> | ||
| Line 51: | Line 66: | ||
<tr> | <tr> | ||
<td width=100><td width='400'>Here, with a quarter-circle curve, the curve angle is 90°. | <td width=100><td width='400'>Here, with a quarter-circle curve, the curve angle is 90°. | ||
| − | + | With a chord of a given length :<br> | |
| − | + | - the more open the curve, the smaller the angle. <br> | |
| + | - the tighter the curve, the greater the angle.</td> <td>[[File:img402.jpg]]</td> | ||
</tr> | </tr> | ||
</table><br><br> | </table><br><br> | ||
| + | |||
| + | <br><br> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td width =100> | ||
| + | <td> | ||
| + | <span style="line-height:20pt;"> | ||
| + | The parameter <b>'Superelevation Degree'</b> is depicted in the game as : the degree of superelevation of this track vertex (where 0 is none, and 1 is one degree bank per degree of curvature).<br> | ||
| + | This means that, for a curve with a chord equal to 200 metres, with a degree of curvature of 45 and superelevation angle of 4.6°, the variable Superelevation Degree should be 4.3/45 = 0.095.<br> | ||
| + | In the game, if we enter this value, the slope observed will be close to 0 metres. In reality, if we want a slope angle of 4.6°, we need to enter a <b>Superelevation Degree</b> = 25 !<br> | ||
| + | To calculate the correct Superelevation values, see the next section. | ||
| + | </span> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br><br> | ||
| + | |||
| + | == '''Superelevation: how do we go about it?''' == | ||
| + | <br> | ||
| + | To proceed to the calculations, download and save to your hard drive the spreadsheet [https://1drv.ms/x/s!ApXRYIL4PqiQgfw2GrkLnD5vr44iyg?e=4DGwip Here] | ||
| + | |||
| + | |||
| + | Proceed in two steps : | ||
| + | * measure the chord and arrow of your curve | ||
| + | * proceed to the calculations with the spreadsheet<br><br> | ||
| + | <u>Measure the chord and arrow of your curve :</u><br> | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td width=100><td width=' | + | <td width=100><td width='800'>In your Asset Pallet, select the spline 'ruler' <kuid:447125:108> Ruler Metric or <kuid:447125:109> Ruler Imperial |
| − | + | Measure the lengths of the chord and the arrow as shown opposite | |
| − | + | </td> <td>[[File:img399.jpg]]</td> | |
</tr> | </tr> | ||
</table> | </table> | ||
<br><br> | <br><br> | ||
| − | = | + | <u>Procced to the calculations whith the spreadsheet :</u><br><br><br> |
| + | <table> | ||
| + | <tr> | ||
| + | <td width=100><td width='820'> | ||
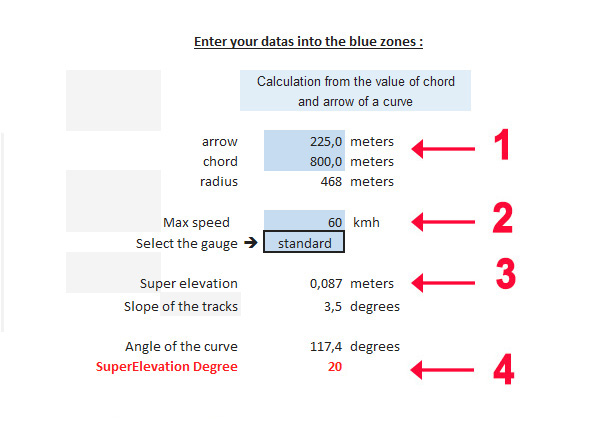
| + | *Enter the values of chord and arrow (1)<br> | ||
| + | *Indicate the maximum speed in the bend and choose between 'standard' or 'metric' gauge (2)<br> | ||
| + | *Look at the value of SuperElevation now displayed (3) : it doesn't have to exceed 16 cms (6.3 inches) in standard gauge tracks and 10 cms (3.94 inches) in metrics -French standard-. If these values are exceeded, reduce the Max speed.<br> | ||
| + | *Note the value of superelevation degree (4) and complete the property <b>'Superelevation Degree'</b> of your track as shown in the first section. | ||
| + | |||
| + | *Also complete the second property <b>'Superelevation Limit'</b> : you can leave this variable equal to 100 since superelevation is controlled by the ‘Superelevation degree’ variable. | ||
| + | </td> <td>[[File:img401_4.jpg]]</td> | ||
| + | </tr> | ||
| + | </table><br><br> | ||
<br> | <br> | ||
| − | |||
| − | + | ==For those who are curious...== | |
| − | * | + | |
| − | * | + | The spreadsheet is based on the following observations:<br> |
| + | * <span style="line-height:16pt;">With a given chord length and a curve angle of 90°, the calculated SuperElevation Degree will apply to any curve with the same chord length, whatever its curve angle.<br> Example: for a 90° bend with a chord length of 200 metres and a bank angle of 8°, we calculate a SuperElevation Degree = 21.5. <br> In Trainz, if this same bend were to be transformed to have an angle of 45°, the SuperElevation Degree = 21.5 value would still apply to produce a bank angle of 4.3°, the desired value. | ||
| + | * For a curve with a given chord and angle, there is a strict correlation between the Superelevation Degree value and the degree of slope required.<br> Example: for a 90° curve and chord = 200 metres, a Superelevation Degree of 10 gives a slope angle of 4°, a Superelevation Degree of 20 gives a slope of 8°, etc... | ||
Latest revision as of 00:09, 11 October 2024
Contents |
[edit] What is superelevation in Trainz 22?
The "superelevation" or the slope of rails in curves is proposed since T:ANE. This page updates the instructions for Trainz 22
Important to note : The ‘Superelevation’ function worked very well with T:ANE and Trainz 2019. As of today (2024 october the 9th), it does not work with Trainz 22 and Trainz PE. This error has recently been rectified and Superelevation is now available again, but for Trainz 22+ owners only.
To resist centrifugal force and and not to wear out prematurely the outer rail, the track must be tilted on bends.
Applying a gradient to a curved section of track is called superelevation.
Here is the example of a machine launched to 80 kph in a curve of 500 meters of beam. The slope of the track has been set to 4 °.
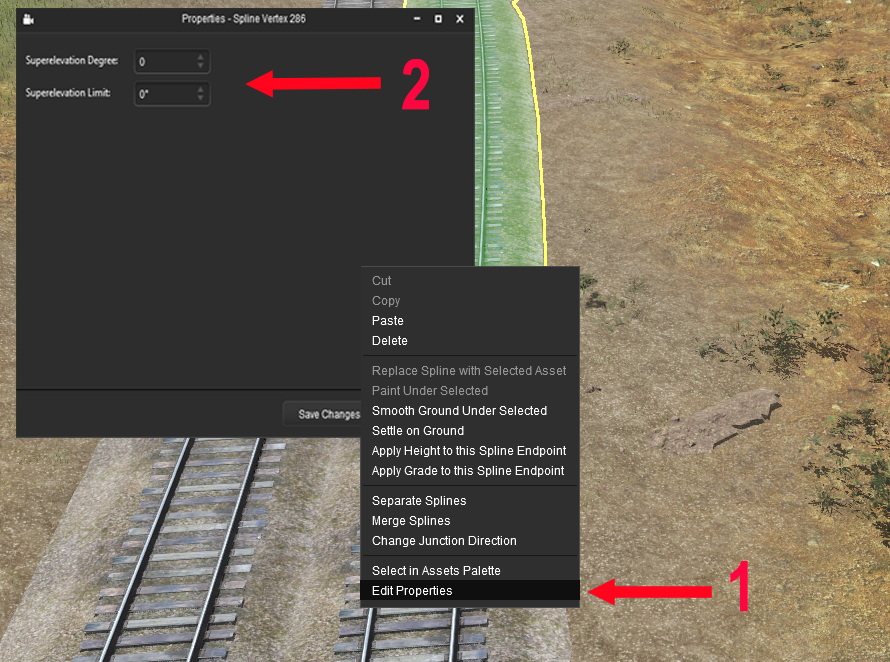
To implement Superelevation in Trainz 22, follow the steps below :
| On the tools palette,select the highlighted icone as shown on the opposite picture (1)
Clic on the track to select it (2) Clic on one of the submits of the selected track (3) |  |
| Clic on Edit Properties (1)
Complete both sections (2) |  |
[edit] Surperelevation : theoritical base
Everything that follows in this section is designed to give you the theoretical basis for calculating a superelevation.
In the next section, a spreadsheet will be provided to do all the calculations for you.
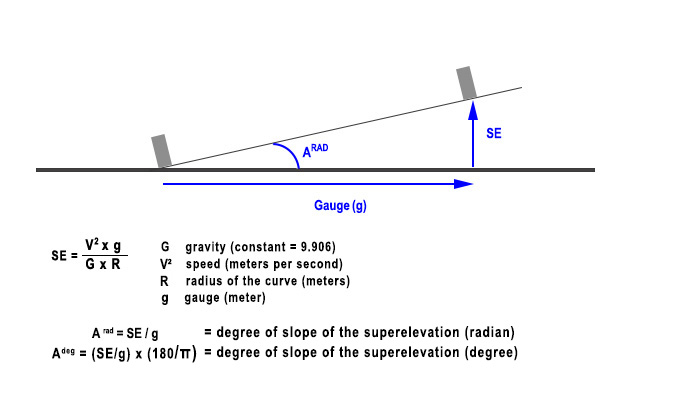
- The Superelevation (SE) is the height that the outside rail takes compared with the internal rail in a curve.
It is calculated as the diagram below shows it:
 |
1 - Maximum value of SE is limited to 16 cm (6.3 inches) for standard gauge tracks and 10 cm (3.14 inches) for metric tracks. |
- Of the four variables above (G, V, R,g), one is unknown at start: the radius of the curve.
The diagram below shows how to determine it :
- Trainz 22 introduces an aditionnal concept for determining the superelevation of a curve: the degree of curvature.
| Here, with a quarter-circle curve, the curve angle is 90°.
With a chord of a given length : |  |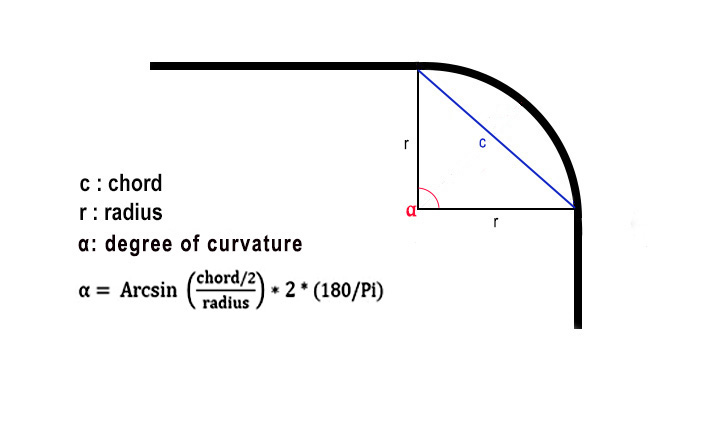
|
The parameter 'Superelevation Degree' is depicted in the game as : the degree of superelevation of this track vertex (where 0 is none, and 1 is one degree bank per degree of curvature). |
[edit] Superelevation: how do we go about it?
To proceed to the calculations, download and save to your hard drive the spreadsheet Here
Proceed in two steps :
- measure the chord and arrow of your curve
- proceed to the calculations with the spreadsheet
Measure the chord and arrow of your curve :
| In your Asset Pallet, select the spline 'ruler' <kuid:447125:108> Ruler Metric or <kuid:447125:109> Ruler Imperial
Measure the lengths of the chord and the arrow as shown opposite |  |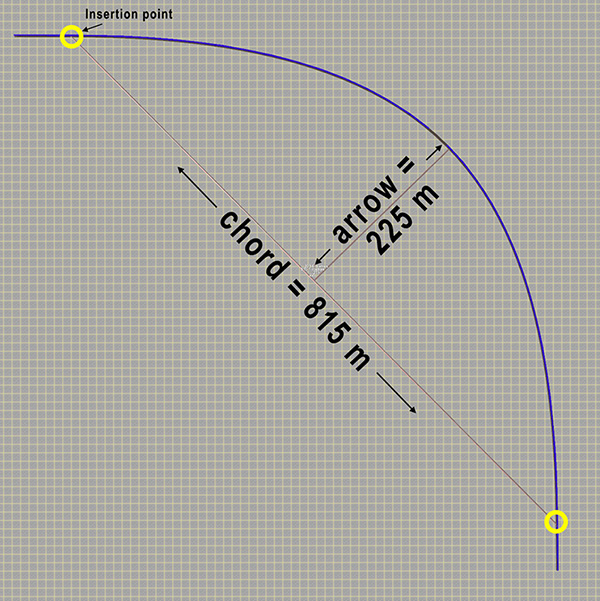
Procced to the calculations whith the spreadsheet :
|  |
[edit] For those who are curious...
The spreadsheet is based on the following observations:
- With a given chord length and a curve angle of 90°, the calculated SuperElevation Degree will apply to any curve with the same chord length, whatever its curve angle.
Example: for a 90° bend with a chord length of 200 metres and a bank angle of 8°, we calculate a SuperElevation Degree = 21.5.
In Trainz, if this same bend were to be transformed to have an angle of 45°, the SuperElevation Degree = 21.5 value would still apply to produce a bank angle of 4.3°, the desired value. - For a curve with a given chord and angle, there is a strict correlation between the Superelevation Degree value and the degree of slope required.
Example: for a 90° curve and chord = 200 metres, a Superelevation Degree of 10 gives a slope angle of 4°, a Superelevation Degree of 20 gives a slope of 8°, etc...
